For example, the probability of blood type O among black people in the United States is 0.49, and the probability that a randomly chosen Japanese person has blood type O is only 0.3). Let’s review the relative frequency method for finding probabilities. The probability of landing the ball on Red can be calculated by dividing the number of red slots by the total number of slots. In this case that would be 18/38, which makes 0.47, or 47%.

• Perhaps the most famous example of the gambler's fallacy occurred in a game of roulette at the Monte Carlo Casino on August 18, 1913, when the ball fell in black 26 times in a row. This was an extremely uncommon occurrence: the probability of a sequence of either red or black occurring 26 times in a row is ( 18 / 37 ) 26-1 or around 1 in 66.6.
• This is an example of an “and” probability. You need to get heads on the first throw AND on the second throw to win this bet. When calculating a probability for multiple events that use the word “and”, you multiply the probability of event 1 by the probability of event 2.

Home- Strategy- Probability- Analysis- Test- Quiz System- Buy- Contact About

award winner

Which outcome has a higher probability after eight successive Blacks, Black again or Red? By Jacob Kanzen

Probability, the Martingale system and the 'delayed' double-up betting strategy.

At roulette each spin is a new spin and the outcome is never determined by prior spins. After eight successive blacks, a black is as likely to come up as a red. You may argue that the reds and blacks will eventually even out over a long run, and you would be right. Indeed, we are both right.

Let's first analyse why the odds are the same each spin of the wheel even if the outcomes even out over a long run, and then we'll look at the popular 'delayed' double up betting strategy, based on the Martingale system, that has an apparent probability advantage employed by most beginners. In order to simplify the calculations, we will assume that the roulette wheel has no zeros, just 18 red and 18 black slots.

Consider this:

In, say, 1,000,000 roulette spins you would have in theory 500,000 reds and 500,000 blacks appearing. Now, we know they don't come up in turns one at a time, that is, you would expect to see two, three, four or more in a row in either colour to appear. For this analysis we will consider the 'eight blacks in a row sequence' as the typical example.

If you were to count all the occurrences of eight blacks in a row FOLLOWED BY A RED, you will find an equal number of occurrences of eight blacks in a row FOLLOWED BY A BLACK (9+ blacks in a row). You will also find an equal number of eight reds in a row in the same way making the total number of blacks and reds equal. If you have a computer roulette simulator, try it out.

This means that of the 'eight blacks' sets there are 50% eight blacks in a row FOLLOWED BY A RED and 50% eight blacks in a row FOLLOWED BY A BLACK. The same applies to the 'eight reds' sets. Therefore if you bet red after eight blacks in a row or if you bet black after eight reds in a row, you will have a 50:50 chance of getting it right.

This is true no matter how many times black or red come up in a row, because for every occurrence of, say, 8, 10 or 20 blacks in a row FOLLOWED BY A RED there will be one with 8, 10 or 20 blacks in a row FOLLOWED BY A BLACK. You just don't know which of the two sequences will come up first.

After eight blacks in a row, your chances of winning are still 50:50 whether you bet on red or black.

Russian Roulette Probability Calculator

Tip: If you are influenced by previous results, then learn to bet with the outcome and not against it. You will eventually realize that it makes no difference. If anything, the 'law of unequal distribution' will be on your side.

The 'delayed' double up betting strategy:

It is a known fact that many players wait for, say, four blacks in a row to appear and then start betting on red doubling up the bet up to four times (or more) if they lose. They do this believing that they have gained a sequential probability advantage - the four successive blacks with no bet. Indeed if you use this strategy, you will win most of the time and you will probably conclude that you have an advantage.

You would be wrong! Take a look at the following figures:

Starting with one chip, if you double up your bet up to four times on red and win, you would win one chip. If you lose on your fourth doubling up bet, you would lose 15 chips (1 + 2 + 4 + 8 = 15). All it takes is one in 16 attempts that you lose and you would have lost all your 15 wins.

Now, try the same double up strategy but bet randomly on red and black. That is, ignore what came up, just bet at will - sometimes red sometimes black and on different tables (switch tables). All you know is this: If you lose you will double up your bet, up to four times. On a long run you should get the same results as your planned one-colour one-table double up betting strategy.

The reason is that it is not the probability of colour that is at work, it is the probability of losing four times in a row on a 50:50 chance bet, which is 1/2 x 1/2 x 1/2 x 1/2 = 1/16. You would in fact in the long run win 15 times and lose one time every 16 attempts, on average. Net profit = 0.

The Martingale system is in fact based on the probability of losing infinite times in a row.

Although infallible in theory, the Martingale system when applied at roulette on the 'even-money' bets requires a large bankroll (it has been reported that in Casino Monte Carlo, Monaco, red came up 39 times in a row), has a very low return and is a very risky one because of the maximum bet limits imposed by the casinos. If you run out of money or reach the house limit, you can lose a lot with no chance to recover your loss.

Tip: For an efficient betting strategy aim to win more money in fewer winning spins.

Two major factors determine how much you win or lose playing roulette. By managing and controlling these two factors, you can generate an advantage that in the long term can make you a winner and keep you ahead of the casino at all times. Find out what these two factors are and what makes a winning system, in the main strategy page titled Winning at Roulette.

Winning at Roulette
Interesting facts, tips and a system.

Home- Strategy- Probability- Analysis- Test- Quiz System- Buy- Contact About

Rate this page: Roulette Probability Analysis.

Kanzen's roulette strategies info site
Email: admin@kanzen.com (Jacob Kanzen)
URL: http://www.kanzen.com/analysis.html

Note: This page should show on kanzen.com domain (see the http:// or www. at the top of your browser).
If you are caught inside a 'Frame' of another domain, click here to break out.

Home- Strategy- Probability- Analysis- Test- Quiz System- Buy- Contact About

Copyright © Jacob Kanzen See copyright notice.

You want to know how to calculate probability in gambling?

The first step is understanding what the word means.

The word probability has 2 meanings:

1. The likelihood that something will or won’t happen.
2. The branch of mathematics that measures that likelihood.

If you’re a casual gambler, you might have a vague idea that the probability of a win can be measured.

But until you understand the specifics of how to calculate probability, you can’t be considered a sophisticated gambler.

This post explains how to calculate probability in gambling and why it matters to gamblers.

How to Calculate Probability as a Fraction

Whether something will happen can be measured on a scale from 0 to 1. If something can never happen, its probability is 0.

Here’s an example of something with a 0 probability:

You have a standard 6-sided die. It’s numbered from 1 to 6. The probability of rolling a 7 is 0. It’s not possible.

Here’s an example of something with a probability of 1:

You have a trick coin with 2 heads. When you flip the coin, the probability of it landing on heads is 1. (And the probability of it landing on tails is 0.)

Most events have a degree of uncertainty to them, though. You can measure how often you expect those events to happen as a fraction.

Here’s an example:

You flip a normal coin with a heads side and a tails side. The probability of getting heads is 1/2.

The Magic Formula for Calculating a Probability

Roulette Probability Statistics Problem

The formula for calculating that probability is simplicity itself:

You divide the number of ways you can achieve the desired event by the total number of possible events.

In the case of a coin toss, there’s only one way to get heads. But there are 2 possible results.

Roulette Wheel Probability Calculator

1 divided by 2 is 1/2.

This probability can be expressed in any of the following ways:

1. As a fraction.
2. As a decimal.
3. As a percentage.
4. As odds.

Some of these are more useful than others in certain situations. I’ll get into that a little more later in this post.

But for now, let’s convert that 1/2 probability of getting heads into each of those 4 ways:

1. As a fraction, the probability is represented as 1/2.
2. As a decimal, the probability is represented as 0.5.
3. As a percentage, the probability is represented as 50%.
4. As odds, the probability is represented as 1 to 1.

Most of us are familiar with probability represented as a percentage. After all, most people watch the nightly news or at least look at the Internet for the weather report.

And they always express the probability of rain with a percentage.

If there’s a 20% chance of thunderstorms, we know that there’s a roughly 1 in 5 chance of rain, thunder, and lightning.

Bigger Probability Problems

Probability gets more interesting as you start calculating probabilities for multiple events.

Let’s say you want to know the probability of getting heads twice in a row.

This is an example of an “and” probability. You need to get heads on the first throw AND on the second throw to win this bet.

When calculating a probability for multiple events that use the word “and”, you multiply the probability of event 1 by the probability of event 2.

In this case, that can be represented as 1/2 X 1/2 = 1/4.

The probability of getting heads twice in a row is, therefore, 1/4, which can also be expressed as 25%.

Notice that the probability is lower. That’s what happens when you multiply fractions.

Let’s say you want to calculate an “OR” probability instead. This time, let’s use a 6-sided die as an example.

You want to know the probability of rolling a 6 on at least one of 2 rolls.

That’s an example of an “or” probability. You want to know how likely it is that you’ll roll a 6 on the first roll OR on the second roll.

You have 6 possible results, but only 1 of them is the 6. So your probability of rolling a 6 on either roll is 1/6.

In an “or” probability, you add the probabilities together. In this case, that would be represented as 1/6 + 1/6 = 2/6. Of course, most people would reduce 2/6 to 1/3, which is also often expressed as a percentage, 33.33%.

Expressing Probabilities as Odds

The tricky expression of this isn’t as a fraction, a decimal, or a percentage. Most of us are familiar with these expressions. That’s basic math.

But most of us don’t have backgrounds in statistics, so we’re not used to expressing probabilities in odds format.

Here’s how to calculate probability in odds format.

When expressing a probability as odds, you just compare the number of ways something can’t happen with the number of ways it can happen.

If you want to look at the odds of rolling a 6 on a single 6-sided die, you’d look at the number of ways you could possibly roll anything else versus the number of ways you can roll the 6.

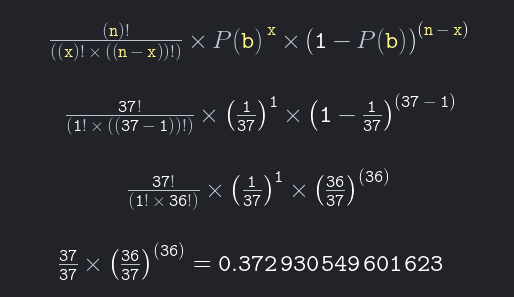
In this case, you’re looking at 5 to 1. You have 5 ways to roll anything but a 6, and only one way to roll a 6.

This becomes useful when you start looking at the expected profit or loss on a bet.

Bets always pay off at certain odds–how much you win versus how much you risk.

Many bets pay off at 1 to 1, or even odds. This is especially true of bets you make in a casual situation.

Here’s an example:

You’re shooting pool at your local bar, and you bet your buddy $20 on the next game. If you win, he gives you $20. If he wins, you give him $20.

But let’s suppose that your levels of skill are different.

Let’s suppose that he’s better than you, and he stands to win 2 out of 3 times.

The odds of him winning are 2 to 1.

If the bet pays off at even odds, in the long run, he’ll profit from playing pool against you under those terms.

He’ll win, on average, $40 during 3 games. You’ll win $20. His net win is $20.

Average that net win out over the 3 games, and he’s winning $6.67 per game on average.

If this were a casino game, you could translate that into a percentage, and you’d have the house edge.

But I’m going to write another post about the house edge, soon. And I don’t want to spoil it for you.

Instead, I’m going to leave you with one more example of how odds are used–this time in a game of poker.

In this example, we’re going to assume that you have 4 cards to a flush, and you’re reasonably sure you’ll win the hand if you make the flush. You’re playing Texas holdem, and you have 2 cards that are hearts in your hand, and there are 2 hearts on the flop.

You have 2 cards yet to come.

You might think that the probability of getting a heart on the next card is 1/4. After all, there are only 4 possible suits in a deck of cards.

But that doesn’t take into account the cards that have already been dealt.

Probability Roulette Wheel Math

You have 2 cards, and there are 3 cards on the board. So there are only 47 cards left.

The deck has a total of 13 hearts in it, but you know that 4 of them are already gone, leaving 9 hearts.

The probability of being dealt a heart for your next card is 9/47.

If you don’t get a card on the next hand, you get another chance, and this time, the probability is 9/46.

The easiest thing to do here is convert those into percentages first.

You have a 19% chance of getting a heart on the turn. You then have another 19% chance, more or less, of getting a heart on the river.

Add those together, and you get 38%. That’s close to 38%, or around 3 to 1.

Blackjack Probability Example

If it costs $100 to get into the pot, you stand to make a profit if the pot has more than $300 in it. If it has less than $300 in it, you stand to lose money over time.

Finally

These are just some rough probability examples. But this is the first step in becoming a savvy gambler–knowing how to calculate probability.

Being able to compare the odds of winning with the odds you’re getting paid enables you to decide whether a bet is profitable.

Not long ago, I wrote about the skills you need to master video poker. Learning how to calculate probability in gambling is included as one of those skills.

Tomorrow I’ll write more about the house edge in casino games.